I wrote this post to make my previous post on camera calibration and triangulation more complete. That post can be found here. Here, I will detail the math behind DLT in the context of 3D point triangulation from multiple camera views. The DLT method is based on singular value decomposition (SVD). If you’re not familiar with SVD, please read up on it first. Also knowledge of homogeneous coordinates is required.

Motivation for DLT DLT is a method for calculating a matrix equation of the form Ax = 0, where A is some matrix and x is the vector unknowns that we want. This problem setting occurs in many forms in photo-grammetry. I will use 3D point triangulation in this post as a motivation.

Suppose we have a 3D point in real space with coordinates given as X = [x, y, z, w] in homogeneous coordinates. Suppose we observe this point through two cameras, which have pixel coordinates U1 = [u1, v1, 1] for cameras #1 and U2 = [u2, v2, 1] for camera #2. Using the camera projection matrix P1, we can write U1 as:

In a triangulation problem, we don’t know the coordinates of X. But we can determine the pixel coordinates and also assume we found the projection matrix through camera calibration. Our tast is then to determine the unknowns in X. Since U1 and P1X are parallel vectors, the cross product of these should be zero. This gives us:

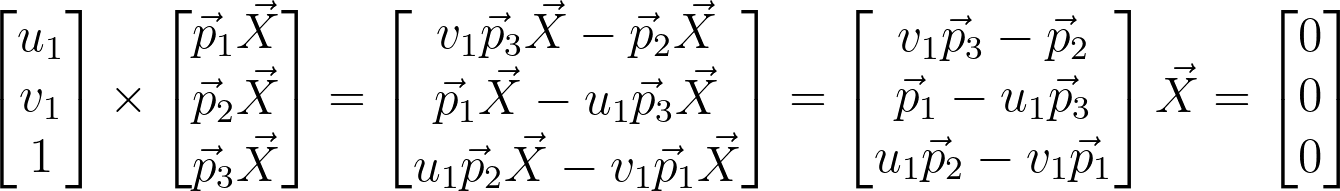
I’ve written the row vectors of P1 as pi, which are 4 dimensional vectors. This gives us an equation of the form Ax = 0. But the third row is a linear combination of the first two rows which then only gives 2 systems of equations, which is not enough to solve the 3 unknowns in X. This is expected, since we can’t determine a 3D coordinate from a single camera view. Since we have two cameras, we can extend the matrix to have more rows. In fact, we simply add on more rows for any number of views. This gives us the equation:

In camera triangulation, we are given A and we want to determine X. In this setting, we use DLT to determine X.

Direct Linear Transform

We want to obtain the non-trivial solution of an equation of the form Ax = 0. In the real world, there can be some noise, so we write the equation as Ax = w, and we solve for x such that w is minimized. The first step is to determine the SVD decomposition of A.

Our goal is to minimize w for some x. This can be done by taking the dot product:

Remember that U and V are orthonormal matrices and S is a diagonal matrix. Moreover, the entries on the diagonal of S are decreasing, so that the last entry on the diagonal is the minimum value. These are guaranteed by the SVD decomposition. Exploiting the property that V is an orthonormal matrix, if we simply select x to be one of the column vectors of V^T:

In the above equation, I’ve written the i’th entry on the diagonal of S as si. Since our goal was to minimize w^Tw, this tells us that it is equivalent to choosing the smallest value of S² by selecting the corresponding v_i column vector of V^T as x. In other words, the minimum value is obtained if we choose the last column vector of V^T as x. Thus we have solved the Ax = w equation in the presence of noise. If there is no noise, this SVD method will still work.

Summary

DLT is used to solve an equation of the form Ax = 0 in the presence of noise. This is easily done by taking the SVD decomposition of A and choosing the last column vector of V^T as x. If you want to see this in action, please see my post on camera calibration and triangulation here.

As a final note, getting the full SVD decomposition of the matrix A to only get one column vector of V^T is not efficient. If you want more efficiency, you might try looking at Shifted Inverse Iterations for specific column vectors of V^T.