This post gives a general strategy on how to calculate joint angles from 3D body poses given in world coordinates. If you need to get 3D body poses, check my post here. If you want to see a demo for calculating joint angles from 3D poses, check my repository here.

There are three main points on how to calculate the joint angles.

1. Obtaining a rotation matrix that rotates one vector to another.
2. Decomposing rotation matrix into rotation sequence along major axes. For example ZXY or XYZ rotation orders.
3. Setting up basic body pose. Also known as T pose.

1. Obtaining a rotation matrix that rotates one vector to another.

We can rotate a general vector A into B by defining a normal direction given AxB and then rotating along this new axis, as shown in Fig. 1. Our strategy is then to change coorindates to the one defined by A, B, AxB, rotate in this basis and then rotate back to original basis.

Figure 1. Rotation along normal direction.

We can define a new basis by making A a unit vector and taking the rejection of B onto A as the second axis. The third axis is simply defined as AxB normalized. This will allow us to write down the change of basis rotation matrix. Once the coordinates are aligned, we can simply rotate along the AxB direction, which is given by Rz rotation matrix. Note however that we don’t need to know the rotation angle, since cos(theta) and sin(theta) are simply dot and cross products of the normalized A and B vectors. The code below calculates the rotation matrix necessary to rotate some vector A into B. Notice however that they don’t have to be the same length, since we normalize the vectors.

#calculate rotation matrix to take A vector to B vector
def Get_R(A,B):

    #get unit vectors
    uA = A/np.sqrt(np.sum(np.square(A)))
    uB = B/np.sqrt(np.sum(np.square(B)))

    #get products
    cos_t = np.sum(uA * uB)
    sin_t = np.sqrt(np.sum(np.square(np.cross(uA,uB)))) #magnitude

    #get new unit vectors
    u = uA
    v = uB - np.sum(uA * uB)*uA
    v = v/np.sqrt(np.sum(np.square(v)))
    w = np.cross(uA, uB)
    w = w/np.sqrt(np.sum(np.square(w)))

    #get change of basis matrix
    C = np.array([u, v, w])

    #get rotation matrix in new basis
    R_uvw = np.array([[cos_t, -sin_t, 0],
                      [sin_t, cos_t, 0],
                      [0, 0, 1]])

    #full rotation matrix
    R = C.T @ R_uvw @ C
    #print(R)
    return R

2. Decomposing rotation matrix into rotation sequence along major axes.

When decomposing a rotation matrix, the order of the rotation is important. In this example, we use the ZXY order, where we rotate around Y first. The rotation matrix in this case is:

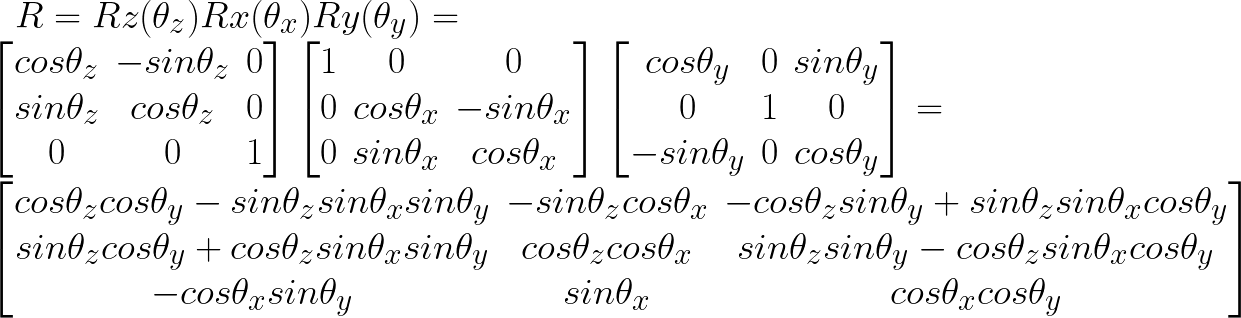
The rotation angles can be calculated from the full expansion above. For example, we see that arctan(r01/r11) gives rotation around z axis. In the same manner, all joint angles are calculated. If any other rotation order is used, then the matrix has to be rewritten with the correct order and then joint angles recalculated. Additionally, the arctan function needs to check the quadrant. Numpy has a useful function that checks the quadrant which I use below.

def Decompose_R_ZXY(R):

    #decomposes as RzRXRy. Note the order: ZXY <- rotation by y first
    thetaz = np.arctan2(-R[0,1], R[1,1])
    thetay = np.arctan2(-R[2,0], R[2,2])
    thetax = np.arctan2(R[2,1], np.sqrt(R[2,0]**2 + R[2,2]**2))

    return thetaz, thetay, thetax

3. Define a T pose.

There are many ways to define the initial pose and to attach axes to each joint. The easiest is to define a T pose as the initial pose and at each joint place axes such that the z axis points forward, as shown in Fig. 2. The end points (wrists, feet) don’t need to have an axes because the position of each joint uses only the rotation matrices of the parent.

Figure 2. Define a T pose and place axes at each joint.

Typically the mid point of the hips are defined as the root joint and everything is defined with respect to it. For example, the left hip would be defined simply as length x (1,0,0) vector and the left knee would be defined as length x (0, -1, 0) vector. Notice that position of any joint is defined with respect to the axes that it is attached to, not the root joint!

To calculate the position of any joint, we have to calculate the position of all of it’s parent joints. This is done by creating a chain of matrix multiplications. For example, to calculate the world position of the foot, we rotate and add all parent joints leading up to the final joint.

Here j vectors are the offsets of each bone with respect to their direct parent. Once these calculations are done for all joints, then we get the world position of all joints. Our task here is given the joint positions in world space, get the joint angles to represent them.

4. Calculating Joint Angles

Suppose we are only given world positions of each joint and need to define the joint angles. We have to decide the root joint and define the rotation of the root joint. This is typically chosen to be the center of the hips. Next, we need to determine the rotation of the root joint. This means we need to place an axes on the root joint. This is done by chosing the left hip as the x axis direction and the neck joint as the y axis direction, which we see makes sense in Fig. 2. Then the z axis is found by through cross product. Once we define the unit vectors of the root joint, we simply center the root joint to zero point of the world coordinate and then rotating to match the T pose.

def get_hips_position_and_rotation(frame_pos, root_joint = 'hips', root_define_joints = ['lefthip', 'neck']):

    """
    frame_pos is a dictionary that contains the current world space position of each joint.
    The root joint is named "hips" here and is the center between the left and right hip positions.
    We can define the x axis as vector pointing from 'hips' to 'lefthip'.
    We can define the y axis as vector pointing from 'hips' to 'neck'.
    """

    #root position is saved directly
    root_position = frame_pos[root_joint]

    #calculate unit vectors of root joint
    root_u = frame_pos[root_define_joints[0]] - frame_pos[root_joint]
    root_u = root_u/np.sqrt(np.sum(np.square(root_u)))
    
    root_v = frame_pos[root_define_joints[1]] - frame_pos[root_joint]
    root_v = root_v/np.sqrt(np.sum(np.square(root_v)))
    
    root_w = np.cross(root_u, root_v)

    #Make the rotation matrix
    C = np.array([root_u, root_v, root_w]).T
    
    #calculate the angles representing the root joint rotations.
    thetaz,thetay, thetax = utils.Decompose_R_ZXY(C)
    root_rotation = np.array([thetaz, thetax, thetay])

    return root_position, root_rotation

Once we know the root position and the root rotation angles, we can start calculating the joint angles of each of the joints. To make our life easier, we subtract the root position from every joint position so that our pose is centered at the world space origin. To calculate the joint angles, we start from the joints closest to the root joint. For example, to calculate the rotation matrix of the left hip, we need to use the joint position of the knee.

Here p’s are the coordinates of the joints while j’s are the joint offsets from the parent joint axes. Remember, the inverse of a rotation matrix is simply the tranpose. The final equation represents a rotation of vector j into vector b. Thus we can simply get the joint angle of the rotation by calling the Get_R() function defined above. Once we get the rotation matrix, we call the decomposition function to get the joint angles.

R = Get_R(j, b)
thetaz, thetax, thetay = Decompose_R_ZXY(R)

Note however that as we calculate joint angles of further joints, we need to modify above equations with more inverse rotation matrices. For example, to calculate the rotation matrix of the knee, we have to write:

Closing remarks

In general, joint angles are not unique, depending on how the pose was set up and what kind of angle limits were placed. This means that joint angle are poor information encoders to use for model training. However they are useful for retargeting a pose to a standard skeleton. For example, different subjects will have different body proportions, which leads to different world space coordinates even if they perform the same motion. To get around this, we can calculate the joint angles and the put these joint angles to a standard skeleton, which will get rid of the differences in body proportions. Another use case is if you used some kind of keypoints estimator to get the 3D coordinates but these coordinates are not consistent. For example, the position of the shoulders might shift around because of the inaccuracy of the keypoints estimator. To get around this, again we calculate the joint angles and place them on a standard skeleton.